當你在生活中觀察到一個有趣現象,並思考其中的道理時。你會驚訝地發現我們的宇宙有可以被理解的物理意義。因為我們可以觀察正在發生的事情,確定並發現支配它的規律,並預測在相同或相似的情況下會發生什麼,總結出一套規範這種現象的科學規律,這正是科學所擁有的最獨特的力量和魅力。但科學也有昏暗的角落,我們無法看清角落裡面發生著什麼。科學也並沒有從根本上告訴我們,宇宙最基本的層面是什麼樣的。我們是由點狀粒子組成的嗎?還是幾何結構?我們是宇宙本身的漣漪嗎?後面這幾個問題是我個人的遐想。(哈哈)
而數學是我們認識宇宙最有力的工具,它讓物理學不在停留在理論層面,數學以自己獨特的方式美麗而優雅的表述出了宇宙最基本的規律。在一個看似簡單的拼圖謎題中,我發現了下面這張被稱為“三角形謎題”的圖片。這張圖裡有多少個三角形?92.6%的人答錯了!所以今天我們就來解答這個問題,並總結一個數學規律!
這張圖裡有多少個三角形?92.6%的人答錯了!
上圖中等邊三角形的兩條邊被來自頂點的三條線分割,這裡就有一個問題是:在這副圖中“ 有多少個三角形?”
如果你有興趣的話,在往下看之前也可以試著自己解一下,看看自己的答案是多少。下文中我將為大家解出正確答案,並展示一個漂亮的數學模型。
先說兩個網友的解答
解(1)
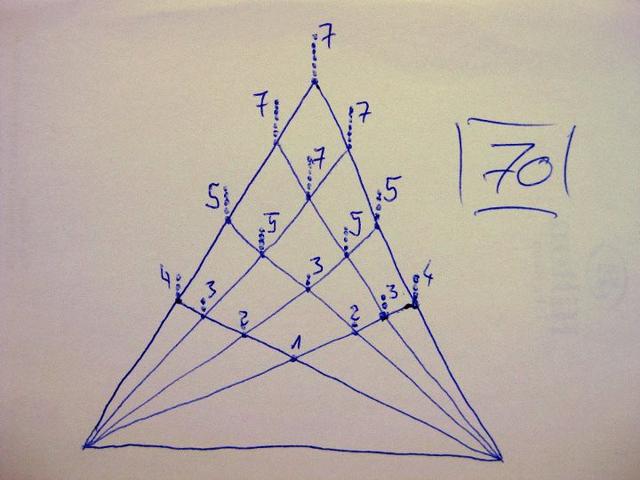
網友的解答
這個方法中嘗試從每條直線相交的每個點構造出新的三角形是可行的,但是這樣在一個圖中數腦子容易亂,很容易將同一個三角形兩次或三次計數。上面圖片中的得出的數字太高了,因為正確答案不是70。
解(2)
可以仔細看上圖這種方法也是特別麻煩,雖然得出了正確答案(劇透警告) 64,但是這個圖解是存在瑕疵的,因為其中沒有算一些實際存在的三角形,可把有些三角形進行了兩次計數。(例如,仔細看第一行、第五行、第六行中被重複計數的三角形)
當你在做題的時候經歷了錯誤的過程卻得到正確的答案時,這其實挺麻煩的,還不如直接做錯。因為能得出正確答案這就說明過程中的錯誤不止一處,需要犯很多錯誤來彌補上一個錯誤,有點讓人頭疼。
這個圖片中到底有多少個三角形
那麼接下來我將通過一個簡單的方法來展示圖中有多少個三角形?
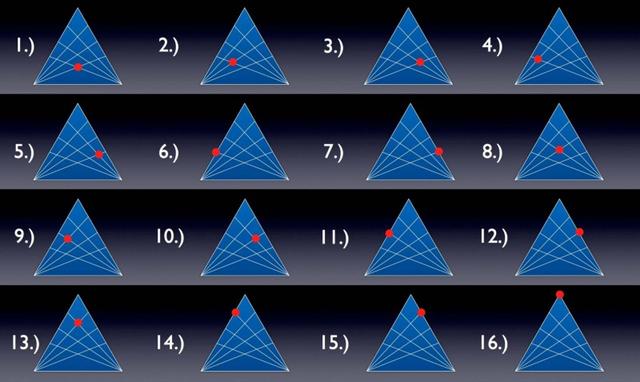
三角形中所有直線相交的點。
我們從三角形的底部兩個基本頂點開始。當我們沿著每條線向上移動時,我們將逐漸遇到兩條線的相交點,上面紅點標記的是我們將遇到相交點的順序。
我們每次遇到相交點時,我們會用相交點和三角形底部的兩個基本頂點中的一個(或兩個)來計算產生的新三角形。為了避免重複計算,我們將只使用當前相交點及以下的點來創建三角形,以確保不會將同一個三角形計算兩次。我們還應該注意下,標記為2和3、4和5、6和7、9和10、11和12、14和15的這些相交點都是彼此的鏡像,所以這些集合給我們提供了相同數量的三角形。
那我們開始吧,通過從1到16這些交點,看看我們得到多少個三角形。
Q1、點1構成的三角形
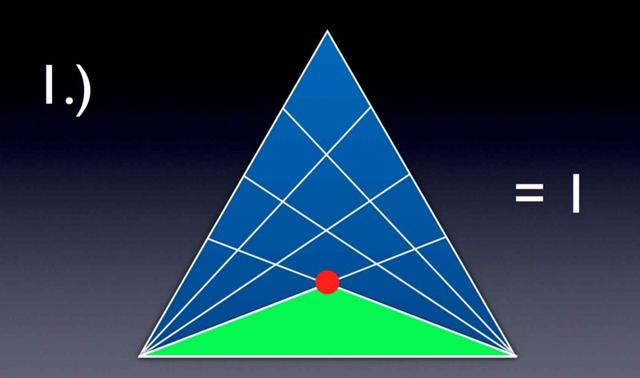
點1作為三角形的頂點
相交點1,是我們到達的第一個點,點1的下方只有兩個基本頂點和它構成了一個三角形,這個很明了,我們開始下一個。
Q2、點2構成的三角形
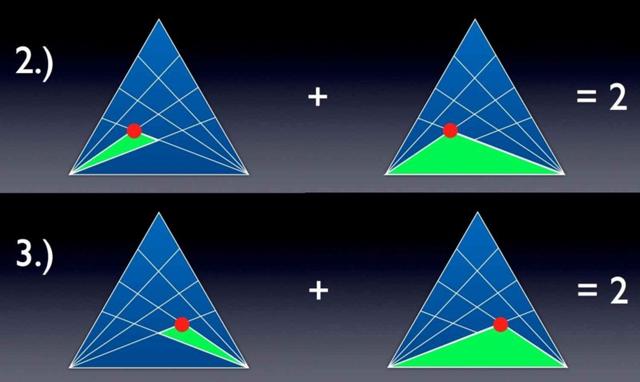
點2和3作為三角形中的頂點。
如圖所示,點2和點3每一個新的相交點都可以構成兩個新的三角形,一個三角形使用的基本頂點,另一個使用相交點—點1,這現在就是構成三角形的一個模式。隨著我們繼續向上找,這種模式會一直繼續下去。
Q3、現在我們來看點4和點5。
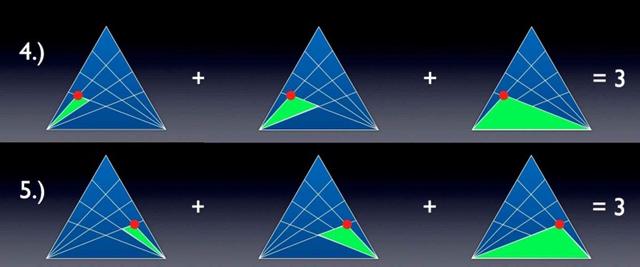
點4和5作為三角形中的頂點。
可以看到,我們可以在每個相交點的下方構造三個新的三角形。這很簡單明了,下面的點6和第7也一樣。
Q4、點6和7構成的三角形
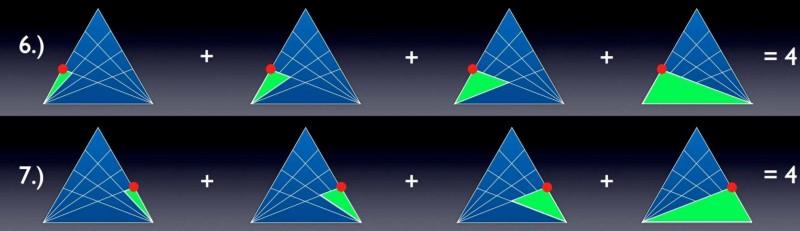
點6和7作為三角形中的頂點。
每個相見點得到四個新的三角形,每個三角形使用的是我們剛才規定的比相交點低的點作為頂點。到目前為止,一切都表現良好:沒有重複計算,也沒有漏掉的三角形。是不是覺得很無趣,覺得沒意思,一點都不好玩。別急,我們再往上走一步,到交叉點8,會稍微有點變化。哈哈!
Q5、點8構成的三角形

點8作為三角形中的頂點。
為什麼點8和上面的點有區別呢?因為,我們現在可以建立成功的,新的,唯一的三角形從相交點8,開始可以連接到比它低的任意一個基本頂點,這是我們以後所有的點都要注意的問題。
Q6、繼續前進,點9和10構成的三角形
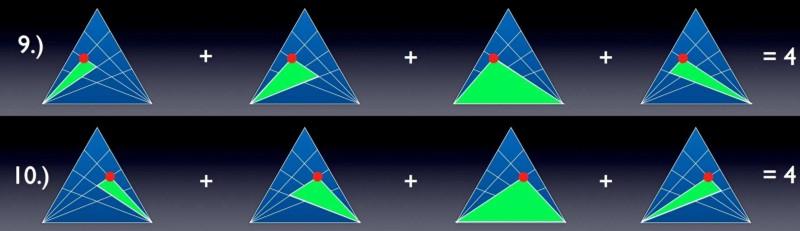
點9和10作為三角形中的頂點。
點9和10分別給出了四個新的、唯一的三角形,分別連接到(或同時連接到)基本頂點(或多個頂點)。
Q7、點11和12構成的三角形
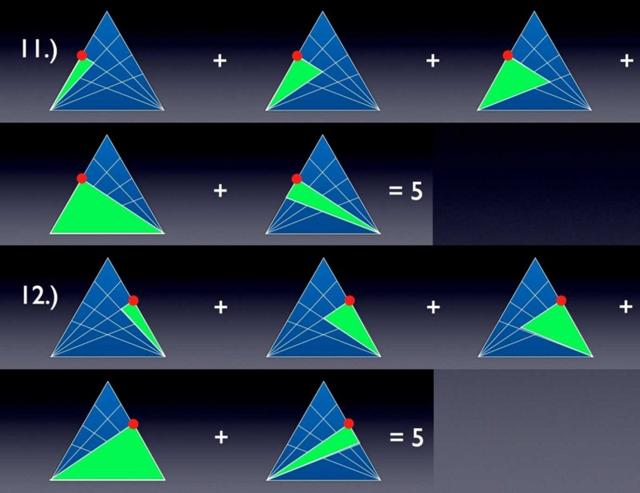
點11和12作為三角形的頂點
對於11和12,我們分別得到了5。到目前為止,所有這些三角形都是唯一的,並且包括了所有三角形。不放心的話請隨意檢查。我們只剩下四個交點了,趕緊數完!
Q8、點13、14、15、16構成的三角形

點13作為三角形中的頂點。
…相交點13再多5個

點14和15作為三角形的頂點。
點14和15各6個,最後,最上面的一點16……
7個!總的來說,我們可以把這些數字加起來,得到1 + 2 + 2 + 3 + 3 + 4 + 4 + 3 + 4 + 4 + 5 + 5 + 5 + 6 + 6 + 7 = 64 ,所以事實上圖片中有64個三角形。別急還沒完!
64是一個神奇的數字:它是一個完美的正方形(8^2 = 64),它也是一個完美的立方體(4^3 = 64),你現在可能想知道三角形的數量是否與兩個基本頂點產生的線數有關。我看看下圖:

在每個新頂點上創建的三角形數
現在,我們將揭開一個規律,三角形的數量恰好和大三角形每個基本頂點下的直線數密切相關,在上面的例子中,大三角形每個基本頂點的下方是4條線。
如果只有一條線,那麼頂點的下方就只有一條直線,也就是說只有一個三角形。
如果我們有兩條直線,那麼每個頂點的下方就是兩條直線,總共有8個三角形。(1 x 1 + 2 x 2 + 3 x 1 = 8)
如果我們只有三條,我們會得到每個頂點的下方會有三條線,總共27個三角形。(1 x 1 + 2 x 2 + 3 x 3 + 4 x 2 + 5 x 1 = 27)
可以看到,對於4條線,我們得到了64。(1 x 1 + 2 x 2 + 3 x 3 + 4 x 4 + 5 x 3 + 6 x 2 + 7 x 1 = 64)
我相信你敏銳的直覺已經註意到了,1^3 = 1、 2^3 = 8 、3^3 = 27 、4^3 = 64,這就是規律!
所以繼續畫一個三角形來自兩個頂點任意數量的直線;現在你不僅知道了基本分析模式,包括向上移動時每個頂點可以生成多少三角形,而且還知道了怎樣一口氣寫出完美的數學公式:n ^3,n是三角形基本頂點下方的線數,直接數就完事了!